3. Trigonometry
f. Applications of Trig Functions
On the previous page, we solved SAS, ASA and SSS triangles. What about other triangles? Here is a list of all possible cases and what we do in each case.
We know \(3\) angles.
With \(3\) angles, there is no way to find the \(3\) sides because similar triangles can have any size as long as the sides are in the appropriate ratios. We can find the ratios by taking one side to be \(1\) and finding the other \(2\) sides using ASA.
We know \(1\) side and \(2\) angles.
We can subtract the \(2\) angles from \(180^\circ\) to get the third angle. Then this reduces to the ASA case discussed on the previous page.
We know \(2\) sides and \(1\) angle.
If the angle is between the \(2\) sides, this is the SAS case discussed on the previous page.
If the angle is not between the \(2\) sides, this is the ASS case discussed on this page. In this case, there may be two solutions, one solution or no solutions.
We know \(3\) sides.
This is the SSS case discussed on the previous page.
2. Solving Triangles- Almost (Optional)
Solving ASS Triangles
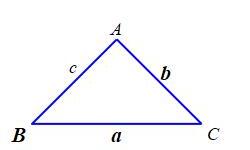
Solve a triangle where we know \(2\) sides of a triangle and an angle which is not between them. We'll take the \(2\) sides to have lengths \(a\) and \(b\) and the angle to be \(B\) opposite the side \(b\).
Figure 1 shows such a triangle with the known quantities in bold. We start to solve the triangle by using the Law of Sines to find \(A_1\): \[\begin{aligned} \sin A_1&=\dfrac{a}{b}\sin B \qquad\qquad (*) \\ A_1=&\arcsin\left(\dfrac{a}{b}\sin B\right) \end{aligned}\] Then we find \(C_1\) by subtracting from \(180^\circ\): \[ C_1=180^\circ-A_1-B \] Finally, we find \(c_1\) by again using the Law of Sines: \[ c_1=\dfrac{\sin C_1}{\sin B}b \]
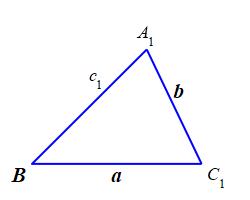
It appears that we have solved the triangle, but this is not the whole story. Equation (*) actually has \(2\) solutions!
Figure 2 shows a second triangle with the same \(a\), \(b\) and \(B\). In Figure 1, \(A_1\) is acute. In Figure 2, \(A_2\) is obtuse.
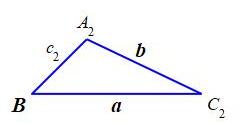
If we superimpose the two figures, we see the triangle \(\triangle CA_1A_2\) is isosceles. So the two base angles are equal and hence \(A_2=180^\circ-A_1\). By the Supplementarity Identity: \[ \sin A_2=\sin(180^\circ-A_1)=\sin A_1 \] So both \(A_1\) and \(A_2\) satisfy (*)!
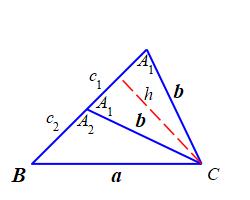
We proceed to solve the second triangle: \[\begin{aligned} C_2&=180^\circ-A_2-B \\ c_2&=\dfrac{\sin C_2}{\sin B}b \end{aligned}\] So we have solved the triangle and found \(2\) solutions.
Notice that in Figure 3, the altitude of the isosceles triangle \(\triangle CA_1A_2\) has been drawn with a dashed line and has length \(h=a\sin B\). We get two solutions because the side \(b\) is greater than the altitude: \[ b \gt h=a\sin B \] If this is not satisfied by \(a\), \(b\) and \(B\), then there would not be two solutions!
There is also an extreme case, shown in Figure 4, where \(A_1=A_2=90^\circ\), and there is only one solution. It is a right triangle with \[ b=a\sin B \]
Finally, there is a beyond the extreme case (Buzz Lightyear's favorite!). If \(b \lt a\sin B\), then side \(b\) is not long enough to reach the third side, as shown in Figure 4, and there are no solutions!
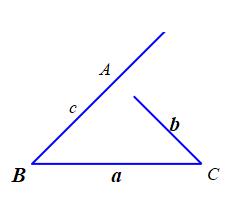
We can visualize this a little better. Draw the angle \(B\) and the side of length \(a\) to the point \(C\). Draw a circle of radius \(b\) centered at \(C\). If this circle just touches the other side of angle \(B\), there is a unique triangle, If it touches in \(2\) places, there are \(2\) triangles. If it does not touch at all, there are no triangles. Click to add this circle to figures 3, 4 and 5.
Find all triangles with sides \(a=4\) and \(b=3\) and an angle \(B=45^\circ\) adjacent to side \(a\) but not side \(b\).
Follow the procedure given above. When you use the Law of Sines, be sure to check to see if there are \(2\), \(1\) or \(0\) solutions.
There are \(2\) triangles. The first triangle has sides: \[ a=4 \qquad b=3 \qquad c_1=3.83 \] and angles: \[ A_1=70.53^\circ \qquad B=45^\circ \qquad C_1=64.47^\circ \] The second triangle has sides: \[ a=4 \qquad b=3 \qquad c_2=1.83 \] and angles: \[ A_2=109.47^\circ \qquad B=45^\circ \qquad C_2=25.53^\circ \]
We will denote the unknown angles and side of the first triangle by \(A_1\),
\(C_1\) and \(c_1\), and those of the second triangle (if there is one) by
\(A_2\), \(C_2\) and \(c_2\).
We start by using the Law of Sines to find \(A_1\):
\[
\sin A_1=\dfrac{a}{b}\sin B=\dfrac{4}{3}\sin 45^\circ\approx 0.94281 \qquad (*)
\]
The acute solution is:
\[
A_1=\arcsin(0.94281)=70.53^\circ
\]
Then we find \(C_1\) by subtracting from \(180^\circ\):
\[
C_1=180^\circ-70.53^\circ-45^\circ
=64.47^\circ
\]
Finally, we find \(c_1\) by again using the Law of Sines:
\[
c_1=\dfrac{\sin C_1}{\sin B}b
=\dfrac{\sin 64.47^\circ}{\sin 45^\circ}3
=3.83
\]
However, there is also an obtuse soluiton to (*):\
\[
A_2=180^\circ-A_1=180^\circ-70.53^\circ=109.47
\]
Next we find \(C_2\) by subtracting from \(180^\circ\):
\[
C_2=180^\circ-109.47^\circ-45^\circ=25.53^\circ
\]
Finally, we find \(c_2\) by again using the Law of Sines:
\[
c_2=\dfrac{\sin C_1}{\sin B}b
=\dfrac{\sin 25.53^\circ}{\sin 45^\circ}3=1.83
\]
There are \(2\) triangles.
tc
These triangles are drawn in Figures 1 and 2 above.
Find all triangles with sides \(a=4\) and \(b=2\) and an angle \(B=45^\circ\) adjacent to side \(a\) but not side \(b\).
There is no triangle.
We start to solve the triangle by using the Law of Sines to find \(A\): \[ \sin A=\dfrac{a}{b}\sin B=\dfrac{4}{2}\sin 45^\circ=\sqrt{2}\approx 1.414 \qquad (*) \] Since this is bigger than \(1\), there is no solution and no triangle.
tc
This is the non-triangle drawn in Figure 5 above.
Find all triangles with sides \(a=4\) and \(b=2\sqrt{2}\) and an angle \(B=45^\circ\) adjacent to side \(a\) but not side \(b\).
There is exactly \(1\) triangle. The sides are: \[ a=4 \qquad b=2\sqrt{2} \qquad c=2\sqrt{2} \] And the angles are \[ A=90^\circ \qquad B=45^\circ \qquad C=45^\circ \]
We start to solve the triangle by using the Law of Sines to find \(A\): \[ \sin A=\dfrac{a}{b}\sin B=\dfrac{4}{2\sqrt{2}}\sin 45^\circ=1 \qquad (*) \] The only solution is \(A=90^\circ\). Then we find \(C\) by subtracting from \(180^\circ\): \[ C=180^\circ-90^\circ-45^\circ=45^\circ \] Finally, we find \(c\) by again using the Law of Sines: \[ c=\dfrac{\sin C}{\sin B}b=\dfrac{\sin 45^\circ}{\sin 45^\circ}2\sqrt{2} =2\sqrt{2} \] Since this is a \(45^\circ\) right triangle, it is not surprising that \(c=b\).
tc
This is the triangle drawn in Figure 4 above.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum